פונקציות ה-random המוכרות נותנות לנו התפלגות אחידה של תוצאות. מה עושים אם צריך דווקא התפלגות בצורת פעמון, או בשמה המקצועי "התפלגות נורמלית"? הנה פתרון פשוט, היישר משיעורי המבוא לסטטיסטיקה.

כשאנחנו מדברים על מספרים אקראיים בהקשר של ארדואינו, הכוונה בדרך כלל לפלט של הפונקציה random: מספרים שלמים, שאינם צפויים מראש, בין אפס (כולל) לבין גבול עליון כלשהו שאנחנו בוחרים. אחת התכונות של random – ולמעשה, זו תכונה קריטית – היא שהתפלגות המספרים אחידה. כלומר, לכל מספר בטווח שבחרנו יש סיכוי שווה להופיע, ואם נספור לאורך זמן את ההופעות של כל מספר בטווח, הערכים יהיו פחות או יותר שווים. להמחשה, חישבו על הטלת מטבע או קוביה.

אלא שלא כל התופעות האקראיות במציאות תואמות להתפלגות אחידה. לדוגמה, גובה של בני אדם בוגרים: בטווח 160-180 ס"מ יהיו הרבה יותר אנשים מאשר בטווח 200-220 או בטווח 120-140 ס"מ, אף על פי ששלושת הטווחים הנ"ל הם ברוחב שווה. גובה של אנשים הוא אחד המדדים שמתפלגים (פחות או יותר) בצורה מפורסמת מאוד, שנקראת "התפלגות נורמלית". בהתפלגות נורמלית, הסיכוי של ערך מסוים להופיע יורד ככל שהערך רחוק יותר מהממוצע, והירידה הזו בסיכוי אינה לינארית (מה שייצור התפלגות בצורת משולש) אלא מורכבת יותר. כדי לתאר אותה בנוסחה מתמטית נזדקק לפעולות חזקה ושורש ולמספרים בעלי נקודה עשרונית.

וכאן מתחילה הבעיה שלנו. אם נרצה לדמות, במיקרו-בקר 8-ביט, תופעה אקראית בעלת התפלגות נורמלית, נוסחאות "לפי הספר" יגזלו מאיתנו המון משאבים – עד כדי האטה בלתי נסבלת ביישום.

כרגיל, יש כמה דרכים לגשת לבעיה כזו ולפתור אותה. הדרך שאציג כאן משתמשת במשפט הגבול המרכזי, שאמור להיות מוכר לכל מי שלמד מעט סטטיסטיקה. לפי משפט זה, כאשר מחשבים ממוצעים של ערכים אקראיים שנלקחים מהתפלגויות אחידות (במובן שהצגתי למעלה), התפלגות הממוצעים האלה מתקרבת בעצמה להתפלגות נורמלית. למה? נדמיין שוב קוביה: בזריקה אחת, הסיכוי לקבל 1 הוא שישית. בשתי זריקות, הסיכוי שהממוצע יהיה 1 הוא 1/36 (שישית כפול שישית). בשלוש זריקות 1/216 וכן הלאה. ככל שאנחנו ממצעים יותר זריקות, כך הסיכוי לקבל ערכים קיצוניים הולך וקטן, והסיכוי לקבל ערכים שקרובים לתוחלת (=ממוצע של אינסוף זריקות) הולך וגדל.

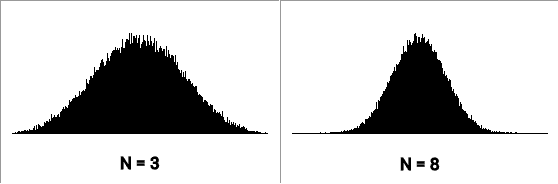
המשמעות של זה בתכל'ס היא שכדי להפיק ערך אקראי שתואם התפלגות נורמלית, אנחנו צריכים רק לקחת כמה ערכים אקראיים מהתפלגות אחידה ולחשב ממוצע שלהם. התוצאות אולי לא יהיו מדויקות לחלוטין מתמטית, אבל בהחלט מספיק טובות לרוב היישומים היומיומיים, ומסתבר שאפילו לא צריך "מדגמים" גדולים במיוחד. ההתפלגות בתמונה שבראש הפוסט (מימין למטה, בשחור), אותה יצרתי בעזרת תוכנית BASIC קטנה שכתבתי, נוצרה מ-50,000 מדגמים של 5 ערכים כל אחד.

ערכי הקיצון של התפלגות נורמלית שהופקה בדרך זו יהיו זהים לערכי הקיצון של ההתפלגות האחידה, כך שקל מאוד לשלוט בהם, והממוצע יהיה בחצי הדרך בין הערך הנמוך לגבוה (שימו לב והיזהרו, כמובן, אם אתם בוחרים טווח קצר ומעגלים את התוצאות). סטיית התקן של ההתפלגות – עד כמה היא "רחבה" או "צרה" – קשורה למספר הערכים שאנחנו ממצעים, ויותר קשה לכוון אותה במדויק.

מצד שני, כמו תמיד, אם היישום שלכם מגיע לרמה כזו שהוא מצריך שליטה מדויקת בסטיית תקן של התפלגות נורמלית, אתם אמורים ממילא כבר להשתמש במיקרו-בקר חזק מספיק בשביל חישובים "לפי הספר"…